二十、用函数实现模块化程序设计

发表于 | 更新于: | 分类于 ， ， |
| 字数: 2.8k | 时长 ≈ 11 分钟

二十、用函数实现模块化程序设计

20.1 函数的初步

用function关键字定义一个函数。所谓的函数，就是一些语句的封装。函数必须调用才能够执行里面的语句。

函数不调用等于白写！！！

函数有两步：定义和调用

1
2
3
4
5
6
7
8
9
10
11
<script>
    // 定义一个函数，函数的名字是haha。注意函数的命名规范，和变量一样
    function haha(){
      alert("哈哈哈哈");
      alert("哈哈哈哈哈哈啊哈哈哈哈哈");
    }

    // 调用函数使用圆括号
    haha();
    haha(); // 调用几次执行几次
</script>

UCuaPH.png

上面的程序，使用function关键字定义了一个函数。function后面加空格，再加函数名字，跟一个圆括号。

1
2
3
function 名字(){
   函数体;
}

函数里面的语句不会执行，必须等到函数被调用。加圆括号就表示调用函数。

1
函数();

20.2 认识函数的参数

1
2
3
4
5
6
7
8
9
10
11
12
13
<script>
    // 定义一个函数，函数的名字是sum。注意函数的命名规范，和变量一样
    function sum(a, b){
      alert("两个数字的和是：" + (a + b));
    }

    // 调用函数使用圆括号
    sum(4, 5)           // 弹出 9
    sum(3, 2)           // 弹出 5
    sum()           // 弹出 NaN
    sum(2, 4, 4, 5, 3, 2, 3)           // 弹出 6    只用前两个，后面的不用

</script>

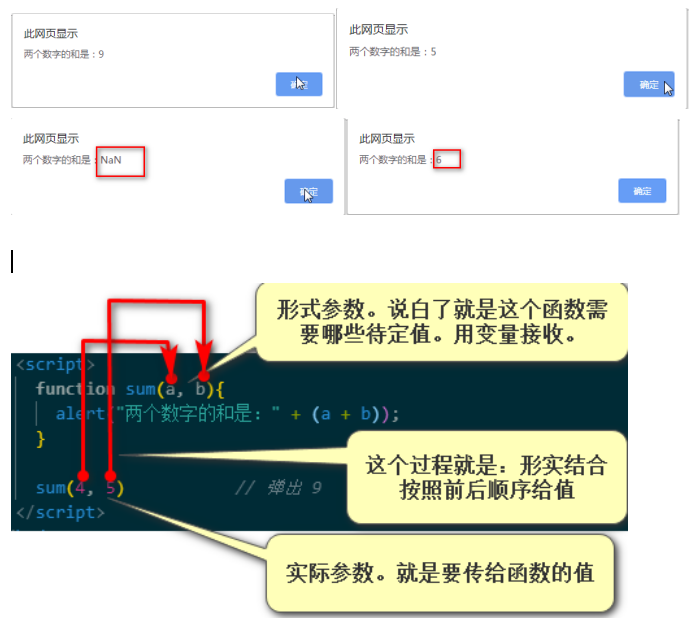
UCKPoD.png

JavaScript中，传参数，全凭自觉。如果参数传的数量不够，或者多了，都不会报错。但是引发程序的不符合预测的运转。

多一个形参，就要多一个实参

1
2
3
4
5
6
7
<script>
    function sum(a, b, c){
      alert("三个数字的和是：" + (a + b + c));
    }

    sum(4, 5, 2)           // 弹出 11
</script>

20.3 return函数的返回值

函数内部可以有return，表示函数的返回值。

一个函数，如果遇见了return语句，则不再继续执行函数体内的其他语句。

如果调用一个内部写了return的函数，必须用变量接收它！！！

1
2
3
4
5
6
7
8
<script>
    function sum(a, b, c){
      // 返回
      return a + b + c;
    }

sum(4, 5, 2);            
</script>

此时运行sum不会有任何弹出

1
2
3
4
5
6
7
8
9
<script>
    function sum(a, b, c){
      // 返回
      return a + b + c;
    }
   // 如果调用一个内部写了return的函数，必须用变量接收它！！！
    var result = sum(4, 5, 2);           // return返回之后，要定义一个变量result来接收这个值
    alert(result);                       // 弹出结果 11
</script>

UCMZh4.png

1
2
3
4
5
6
7
8
9
<script>
    function sum(a, b, c){
      // 返回
      return a + b + c;
    }

      sum(4, 5, 2);          
      alert(sum);                     
</script>

UCM8AO.png

1
2
3
4
5
6
7
8
9
<script>
    function sum(a, b, c){
      // 返回
      return a + b + c;
    }

      sum(4, 5, 2);          
      alert(return);                     
</script>

UCMUgA.png

20.4 为什么要有函数？认识函数的黑箱特性、轮子。

工作时，你的公司以前的项目或多或少封装过一些函数。这些函数普遍提供一些基本功能，比如验证身份证号码是否合规、手机号码是否合规。这些函数，术语叫做“轮子”。

函数只需要关注它需要传入什么，返回什么即可，不需要关心它内部的语法。

比如，网上找一个判断身份证的：

1
2
3
4
function checkID(idnumber){
语句不用关心
语句不用关心
}

我们只需要用：

1
2
var result = checkID(444444199909096666);
alert(result);

例1：写一个函数，这个函数能够返回 a 和 b 之间所有数字的和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
<script>
    // 写一个函数，这个函数能够返回 a 和 b 之间所有数字的和
    function sumAtoB(a, b){
      var sum = 0;
      for(var i = a ; i <= b ; i++){
        sum += i
      }
      return sum;
    }

    // 调用这个函数
      var result =sumAtoB(3, 6);          //计算3+4+5+6的和
      alert(result);                     // 弹出 18
</script>

例2：写一个函数，判断字符串 a 中有没有 b 字符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
<script>
    // 写一个函数，判断字符串 a 中有没有 b 字符
    function checkAStrHaveB(a, b){
      for(var i = 0 ; i < a.length ; i++){
        if(a.charAt(i) == b){
          break;
        }
      }
      return i != a.length;
    }

    // 调用这个函数
      var result =checkAStrHaveB("牛牛牛牛牛牛牛牛牛牛牛午牛牛牛牛牛牛牛牛", "午");     //判断 a 中有没有 b
      alert(result);                     // 弹出结果为真或假
</script>

20.5 为什么要有函数？函数能够拆分逻辑，从大逻辑变化为小逻辑

例1：寻找100~999以内的喇叭花数。

喇叭花数特点：各个数位的阶乘的和，等于它本身。

什么叫做阶乘？比如4的阶乘就是432*1等于24

大逻辑：寻找喇叭花数————→小逻辑：先封装一个函数，能够返回a的阶乘

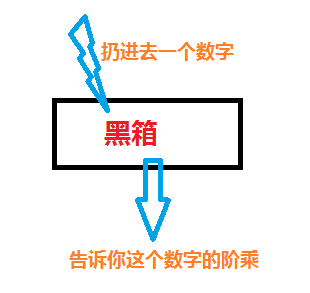
UCMvb6.png

首先封装一个函数

1
2
3
4
5
6
7
8
9
10
11
12
13
<script>
    // 先封装一个函数，能够返回一个数字的阶乘
    function factorial(a){
      // 累乘器
      var result = 1;
      //算阶乘
      for(var i = a ; i >= 1 ; i--){
        result *= i;             // 累乘
      }
      // 返回结果
      return result;
    }        //函数写完后一定要测试，测试时直接在控制台书写factorial(数字a),函数书写正确，则会算出结果
</script>

在控制台进行测试：

UCQGq0.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
<script>
    // 先封装一个函数，能够返回一个数字的阶乘
    function factorial(a){
      // 累乘器
      var result = 1;
      //算阶乘
      for(var i = a ; i >= 1 ; i--){
        result *= i;             // 累乘
      }
      // 返回结果
      return result;
    }        //函数写完后一定要测试，测试时直接在控制台书写factorial(数字a),函数书写正确，则会算出结果
    
    // 寻找喇叭花数
    for(var i = 100 ; i <= 999 ; i++){        //上下两个 i 不冲突，下面的i是重新定义的
      // 拆位
      var baiwei = ~~(i / 100);
      var shiwei = ~~(i /10) % 10;
      var gewei = i % 10;
      // 调用函数
      if(factorial(baiwei) + factorial(shiwei) + factorial(gewei) == i){
        console.log(i + "是喇叭花数")
      }
    }
</script>

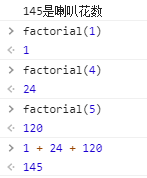
UCQdG4.png

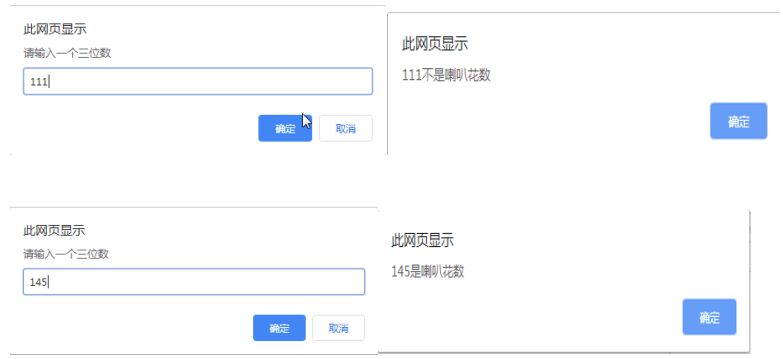
例2：输入一个三位数，判断是不是喇叭花数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
<script>
    // 先封装一个函数，能够返回一个数字的阶乘
    function factorial(a){
      // 累乘器
      var result = 1;
      //算阶乘
      for(var i = a ; i >= 1 ; i--){
        result *= i;             // 累乘
      }
      // 返回结果
      return result;
    }        //函数写完后一定要测试，测试时直接在控制台书写factorial(数字a),函数书写正确，则会算出结果

    // 输入一个数字 i
    var i = prompt("请输入一个三位数");
    
    // 拆位
    var baiwei = ~~(i / 100);
    var shiwei = ~~(i /10) % 10;
    var gewei = i % 10;
    // 调用函数
    if(factorial(baiwei) + factorial(shiwei) + factorial(gewei) == i){
      alert(i + "是喇叭花数");
    }else{
      alert(i + "不是喇叭花数");
    }
</script>

UCQWJe.png

20.6 为什么要有函数？方便制作功能的递进

例1：列出1~50中所有偶数拆分为两个质数和（哥德巴赫猜想）

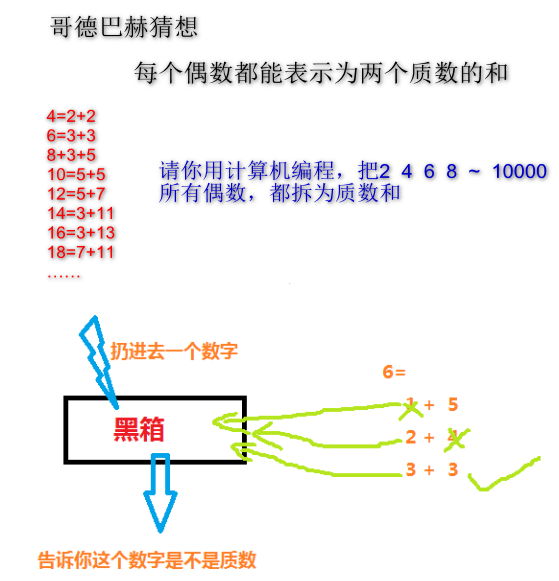
UCQbo8.png

1
2
3
4
5
6
7
8
9
10
// 检测 a 是不是质数，函数返回布尔值
    function checkIsPrime(a){
      for(var i = 2 ; i < a ; i++){
        if(a % i == 0){
          break;
        }
      }
      // 看 i 和 a 是不是相等，如果等就是质数，如果不等就不是质数
      return i == a;
    }

测试：

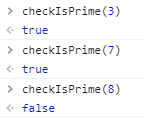
UClkYF.png

递进：

一个函数的基础上，可以演变为更高级别的函数

1
2
3
4
// 检测 a b 是不是都是质数
    function checkBothIsPrime(a, b){
      return checkIsPrime(a) && checkIsPrime(b);
    }

测试：

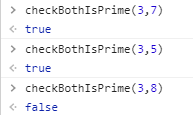
UClKw6.png

1
2
3
4
5
6
7
8
9
10
// 这个函数能够把 n 最小（左边值最小）的一组和（都是质数）输出
    function PrimeSum(n){
      for(var i = 1; i < n ; i++){
        if(checkBothIsPrime(i, n - i)){
          console.log(n + "=" +  i + "+" + (n - i));
          return;   // return;表示当控制台输出一个结果后就结束输出。
                    // 函数遇见return会立即结束
        }
      }
    }

测试：

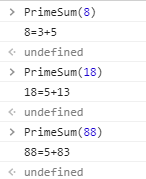
UCla0P.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
<script>
    // 检测 a 是不是质数，函数返回布尔值
    function checkIsPrime(a){
      for(var i = 2 ; i < a ; i++){
        if(a % i == 0){
          break;
        }
      }
      // 看 i 和 a 是不是相等，如果等就是质数，如果不等就不是质数
      return i == a;
    }

    // 检测 a b 是不是都是质数
    function checkBothIsPrime(a, b){
      return checkIsPrime(a) && checkIsPrime(b);
    }

    // 这个函数能够把 n 最小（左边值最小）的一组和（都是质数）输出
    function PrimeSum(n){
      for(var i = 1; i < n ; i++){
        if(checkBothIsPrime(i, n - i)){
          console.log(n + "=" +  i + "+" + (n - i));
          return;   // return;表示当控制台输出一个结果后就结束输出           // 函数遇见return会立即结束
        }
      }
    }

    // 主程序
    for(var i = 2 ; i <= 50 ; i +=2){
      PrimeSum(i);
    } 
</script>

UClylj.png

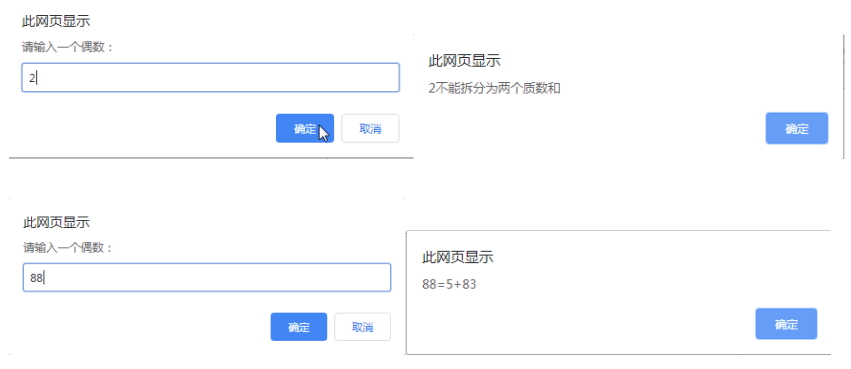
例2：输入一个偶数，给出拆分为两个质数和（哥德巴赫猜想）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
<script>
    // 检测 a 是不是质数，函数返回布尔值
    function checkIsPrime(a){
      for(var i = 2 ; i < a ; i++){
        if(a % i == 0){
          break;
        }
      }
      // 看 i 和 a 是不是相等，如果等就是质数，如果不等就不是质数
      return i == a;
    }

    // 检测 a b 是不是都是质数
    function checkBothIsPrime(a, b){
      return checkIsPrime(a) && checkIsPrime(b);
    }

    // 这个函数能够把 n 最小（左边值最小）的一组和（都是质数）输出
    function PrimeSum(n){
      for(var i = 1; i < n ; i++){
        if(checkBothIsPrime(i, n - i)){
          return n + "=" +  i + "+" + (n - i);
        }
      }
    }

    // 主程序
    var i = prompt("请输入一个偶数：") || 4,
        result = PrimeSum(i);

    if(PrimeSum(i)){
      alert(result);
    }else{
      alert(i + "不能拆分为两个质数和");
    }
</script>

UC19cd.png

20.7 递归函数和递进函数

20.7.1 递归函数

递归函数：在函数内部调用自身，一般解决数学问题

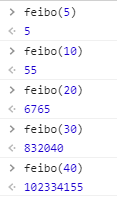
案例：斐波那契数列

斐波那契数列：1,1,2,3,5,8,13,21,34，……

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
<script>
    /* 
    斐波那契数列：1，1，2，3，5，8，13，21，34，……
    目的：用户输入项数，我们返回该项对应的值
    参数：一个项数从第一项开始
    返回值：项数对应的值
     */

     // 函数
     function feibo(n){
       // 用户输入第n项，返回对应的值
       // 从第三项开始，值等于第 n - 1 项对应的值加上 第n - 2 项对应的值
       // 比如，第四项3，第n- 1 项对应的值2，第n-2项对应的值1
       if(n == 1 || n == 2){   // 第 1 项和第 2 项值都是 1
         return 1;
       }else{
        return feibo(n - 1) + feibo(n - 2);     // 递归：在函数里面调用自己
       }
     }
</script>

UC1rE6.png

20.7.2 递进函数

递进函数：一个函数的基础上，可以演变为更高级别的函数

案例：哥德巴赫猜想

哥德巴赫猜想：列出1~50中所有偶数拆分为两个质数和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
<script>
    // 检测 a 是不是质数，函数返回布尔值
    function checkIsPrime(a){
      for(var i = 2 ; i < a ; i++){
        if(a % i == 0){
          break;
        }
      }
      // 看 i 和 a 是不是相等，如果等就是质数，如果不等就不是质数
      return i == a;
    }

    // 检测 a b 是不是都是质数
    function checkBothIsPrime(a, b){
      return checkIsPrime(a) && checkIsPrime(b);
    }

    // 这个函数能够把 n 最小（左边值最小）的一组和（都是质数）输出
    function PrimeSum(n){
      for(var i = 1; i < n ; i++){
        if(checkBothIsPrime(i, n - i)){
          console.log(n + "=" +  i + "+" + (n - i));
          return;   // return;表示当控制台输出一个结果后就结束输出           // 函数遇见return会立即结束
        }
      }
    }

    // 主程序
    for(var i = 2 ; i <= 50 ; i +=2){
      PrimeSum(i);
    } 
</script>

UClylj.png

相关文章
点击查看

本文标题:二十、用函数实现模块化程序设计

文章作者:Mango

发布时间:2020年07月08日 - 21:53:34

最后更新:2020年07月08日 - 22:35:39

原始链接:https://mango185.github.io/post/76c62fe5.html

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

-------------------本文结束 感谢您的阅读-------------------
欢迎光临
❤️
Mango小站
请多关照
❤️
❤️